Edward G. Dunne and Mark McConnell are Wrong aka Noncommutative Phase or why Wikipedia is wrong about the Pythagorean Comma

Edward G Dunne

1:44 PM (21 minutes ago)

to me

Dear Drew Hempel,

Thank you for your message.  I have not thought about the temperament question in a long time.  If I have any comments about your blog post, I will let you know. 

Best regards,

Edward Dunne

to Edward

Yes physics professor Albert Bartlett gave the same lecture 2000 times about the exponential function and the ecological crisis. It all started when music tuning was lied about from Philolaus flipping his lyre around and so hiding the truth about reality, so that Ph.D. professors can wax nostalgic about "temperament." haha. Thanks, drew
https://oeis.org/DUNNE/TEMPERAMENT2.html

This is a very thorough math overview of the Pythagorean comma - getting into continued fractions, logarithms, etc.

https://en.wikipedia.org/wiki/Pythagorean_comma

Now I have defined the Pythagorean Comma as Sir James Jeans defined it in his classic book, Science and Music which is also how this music professor defines it:

This ratio, 129.75632 : 128 is the Pythagorean comma. 12 perfect fifths do not equal up to 7 perfect octaves:

(3/2)^12 ≠ (2/1)^7 or you could say (3/2)^12 / (2/1)^7 ≠ 1.

But if you look at the two above sites - Wiki and the "encyclopedia of integer sequences" article of

This note's for you: A mathematical temperament. Edward G. Dunne. September 15, 2000. -

Pianos and Continued Fractions - OEIS

https://oeis.org/DUNNE/TEMPERAMENT.HTML

Edward G. Dunne. American Mathematical Society. Email: egd@ams.org. It is an old (and well-understood) problem in music that you can't tune a piano ... Edward Dunne and Mark McConnell, Pianos and Continued Fractions, Mathematics Magazine, vol. 1999 ... It should have half the frequency of the G in the second octave.

[PDF]PIANO TUNING AND CONTINUED FRACTIONS 1. Introduction While ...

https://www.whitman.edu/Documents/Academics/Mathematics/bartha.pdf

by M BARTHA - ‎Cited by 2 - ‎Related articles

Next, we use of these fractions to evaluate how pianos are tuned and why one cannot be tuned perfectly. ... in most real-world applications of mathematics, continued fractions are rarely the most practical way to solve ...... (4) ”Pianos and Continued Fractions,” by Edward Dunne and Mark McConnell. Mathematics Magazine ...

you get the equivalence of the Pythagorean Comma with the Ditonic Comma

And Wiki justifies this equivalency with this explanation:

  or the difference between three Pythagorean ditones and one octave (this is the reason why the Pythagorean comma is also called a ditonic comma).

And so what is a Pythagorean "ditone" - it is the major third defined by Perfect Fifths/Octaves (81/64) versus a "just third" as 5/4. And so (81/64 to the third) has a ditone difference to the octave. But I have already quoted music scholars clearly stating that Orthodox early Pythagorean philosophy ONLY uses the Perfect Fifth/Perfect fourth and Octave as the Tetraktys.

“Orthodox Pythagorean theory recognizes five consonances: fourth, fifth, octave, twelfth, and double octave; and these are represented by the multiple and superparticular ratios [n + 1 : n] from the tetrad. The number 8 obviously does not belong to the tetrad.”

André Barbera, "The Consonant Eleventh and the Expansion of the Musical Tetractys: A Study of Ancient Pythagoreanism," Journal of Music Theory, 1984, citing Ptolemy of 2nd century.

From the point of view of perception, as Ptolemy states (11.1-3) and as all parties to these enquiries agree, the fourth, fifth and octave are indubitably concordant, and this property belongs to no other interval within the octave.

Professor Andrew Barker, Oxford, emeritus, p. 58, Scientific Method in Ptolemy's Harmonics

My claim is that in fact Orthodox Pythagorean philosophy was based on what Peter Kingsley details as "incubation" meditation with five years of silence as infinite resonance from noncommutative phase. R. P. Winnington-Ingram's, “Aristoxenos and the Intervals of Greek Music,” (1932) as an article “admits that the pre-Platonic theorists used the tone 8:9 to construct a scale, but for some reason is reluctant to attribute this construction to the Pythagoreans.”

Professor Richard McKirahan reveals the secret:

The word translated epogdoic is not a musical term but a mathematical one. An epogdoic ratio is the ratio of 9 to 8. The occurrence of a mathematical term here is unexpected. It has been treated as an unimportant anomaly but in fact it is the key to the entire fragment....The word magnitude normally refers to physical size, but here it is given a new application, extending the notion of magnitude to include musical intervals.

Or as Professor Borzacchini states:

These remarks raise the question of the difference between the ancient Pythagorean ‘musical’ perception as displayed in the Pythagorean idea of ‘linear number’ in Boethius [Philolaus] or in Nicomachus, and the modern ‘geometrical’ perception of the linear numerical magnitudes.

 And so to define the Pythagorean Comma as Ditonic Comma makes a fundamental error in Pythagorean philosophy. Another way to explain this is that the Ditonic Comma already assumes 8/9 or 9/8 as the fundamental logarithmic ratio of reality as the continuum, whereas this is fundamentally not true for Pythagorean philosophy.

So you have 8 to the 6th power and 9 to the 6th power (531441) based on the rule of doubling/halving for octaves but the ONLY way that the Perfect Fifth - the Perfect Fourth = 9/8 and the Perfect Fifth + the Perfect Fourth = the Octave is to define the Perfect Fifth and Perfect Fourth not as the fractions 3/2 or 2/3 but as the logarithms of 3/2 squared being 9/4 with the Octave 2 defined as the Geometric Mean Squared. This is the subtle difference between multiplying as doubling and squaring as geometric mean.
 So as I have explained - from Professor Richard McKirahan we learn how Philolaus had to flip his  Lyre around so that 3/4 as the Perfect Fourth is the wavelength of 0 to 8 root tonic as 1 while 4/3 is the geometric magnitude of 8/6 as the root tonic of 12 to 0 in the opposite direction as 1. So the question is - is 1 a square inherently as geometry? or is 1 a number that can not be seen but rather listened to. The Orthodox early Pythagoreans taught that 1 is NOT a number but originates from female formless awareness as time that is both odd-even at the same time and "breathes" as the void, creating the One as Light. Math Professor Louis Kauffman understands that 1 originates as a noncommutative time series:

Scientific Essays In Honor Of H Pierre Noyes On The Occasion Of His ...

https://books.google.com/books?isbn=9814579386

Kauffman Louis H, ‎Amson John C - 2013 - ‎Science

The special synchronization is the algebra of the time shift embodied in ηη = 1 and [a, b]η = η[b, a] that makes the algebra of i = [1,−1]η imply that i2 = −1.

So the continued fraction as integer sequence encyclopedia website gives this equation as the Ditonic Comma and again it is equated with the Pythagorean Comma but based on this stipulation:

The stipulation is given in parenthesis - even though it's a MATH website - as it if doesn't really matter:

(start counting at zero):

Oh yeah? REALLY? Now the Harmonic Series in math starts at 1 and diverges but still defines frequency as square root of wavelength divided by PI (assuming commutative phase time). 

The frequency is not simply related to the length when it comes to vibrating bars, like you find on a xylophone or a marimba (the frequency is inversely proportional to the square of the length). Music of the Spheres and the Lessons of Pythagoras

 The Fourier theorem is purely mathematical: (Delta 2 pi f)(Delta t) > ½ but this incorrectly assumes commutative phase time! Either the phase is a "constant cycle" and so can be infinite but it is still symmetrical (known as time-frequency uncertainty, so that the Perfect Fifth can never be precisely measured) or the time as phase converges, again, still incorrectly assuming a geometric magnitude definition of phase! 

For example h-bar means Planck's Constant based on a closed symmetric time phase cycle of h/2 pi aka ħ = h/(2π). But in fact spin 1/2 quanta are noncommutative to one phase cycle of 2 pi and so are converted to 720 degree spin that is symmetric math as the Poisson Bracket, circulating along a closed loop in a given time that is noncommutative! This is the secret cause of the Josephson Junction effect that converts phase into voltage as superconducting energy. In other words time is normally hidden in Planck's Constant as an outside parameter that has instead been converted to symmetric density as phase. And so due to noncommutative phase, de Broglie's Law of Phase Harmony discovered there is a 2nd time operator that is from the future and superluminal, and nonlocal, as a guiding phase wave ether.

This is the origin of the "Measurement problem" at the foundation of physics, since gravity causes "objective" collapse due to the hidden commutative (logarithmic gravity) phase of the spin.

Cycle as wavelength divided by time is converted to frequency = square root of wavelength divided by pi. The time origin is lost as an inherent operator. In other words if the phase is opposite but has the same geometric magnitude (i.e. of Perfect Fifth) then the amplitude can be canceled out - but this is empirically not true! Since frequency is noncommutative to time then 2/3 is C to F phase undertone while 3/2 is C to G phase overtone and so even though their "geometric magnitude" is the same as Perfect Fifth, their relation to the root tonic or fundamental pitch is not the same. The empirical truth is noncommutative phase that is nonlinear resonance (superluminal as G=3=F at the same time). 

So for example the trendy "Neo-Riemannian" torus Tonnetz music analysis claims to be noncommutative but has a diatonic comma in one phase direction while a chromatic ditonic comma phase in the other direction! Both are still constructed from geometric magnitude that is originally commutative symmetric logarithmic math.

 In other words, from Mersenne (and later Newton as his secret of gravity), the wavelength doubled has the same frequency if the mass as density is squared. So 4 times the weight makes twice the frequency based on the square root of the weight. The same tension along a string half as long has 4 times the force.
 

Frequency is directly proportional to the square root of the tension in the string; f µ ÖT; Frequency is inversely proportional to the square root of the mass per unit length of the string; ...

inertia, resonant frequency, stiffness and kinetic ... - Wiley Online Library

onlinelibrary.wiley.com/doi/10.1113/expphysiol.1987.sp003060/pdf

by EG Walsh - ‎1987 - ‎Cited by 18 - ‎Related articles

A significant correlation was found between resonant frequency and the square root of the reciprocal of inertia, a relationship also predicted on theoretical grounds.

Fundamentals of Musical Acoustics: Second, Revised Edition

https://books.google.com/books?isbn=0486150712

Arthur H. Benade - 2012 - ‎Music

"\under tension Lr ) \| d \| 47 For such a string we see that fn = nfi; i.e., the natural frequencies form an exact harmonic series. ... on the other hand, that the frequencies are proportional to the square root of the tension; as a consequence of this it would be necessary to quadruple T in order to raise the pitch of the plucked string ...

In the music overtone series there is no 4/3 (what is called the Phantom Tonic) but Western music then uses the music "harmonic series" that assumes 4/3 as a geometric magnitude ratio, not a rational fraction. See the subtle bait and switch going on!! What is the "phantom tonic" is actually what Einstein called the "ghost waves" of de Broglie - from noncommutative phase, explained by Alain Connes below.

Even Newton realized the secret source of gravity (that he could never explain except through the inverse square law) was from the VOID of Pythagorean alchemy!!

Newton then quotes twelve lines of Book I of De Rerum Natura which state that the void exists, and that of any bodies which are equal in magnitude, difference in weight is explained more or less by interstitial void. [noncommutative phase] Newton's comment on this passage is important:

For he [Lucretius] affirms that fire, and other bodies which are designated weightless, rise upwards not of their own accord but by a force which drives them from below....

Newton and the ‘Pipes of Pan’

J. E. McGuire, P. M. Rattansi,
Notes and Records of the Royal Society 21, 1966

Math professor Luigi Borzacchini and now Professor Richard McKirahan have proven that irrational magnitude was created from music theory - not the other way around! Zero was only created FROM geometric magnitude of music theory!! So you can not define the Pythagorean Comma by assuming zero already exists when real Pythagoreans did not use zero!

And so then when we turn to Chinese music tuning we get this strange "exception."

With the exception of B#, or the ditonic comma,[10] ratio 531441/524288, Table 11.2 shows that the Chinese and Pythagorean progression of ratios are identical, which means that both sequences form an ascending spiral of “fifths.”

Now what is the fundamental difference? This music theory website tries to limit it to a certain scale size based on music pitch or notes. But that is not at all what traditional music tuning in China and with Orthodox Pythagoreans was about at all!! The same is true for India - the three gunas, and in China it is the Emptiness, yang and yin - they are the true philosophy of music intervals, NOT assuming zero exists as created from logarithms, created by the LIE of flipping the Lyre around!! haha.

Tai Chi as Harmonic Series

In other words 2/3 is the Perfect Fifth as C to F subharmonic while 3/2 is the Perfect Fifth as C to G overtone harmonic. So 8/12 is 2/3 as C to G frequency while 6/8 is 3/4 as 4/3 frequency - one is the wavelength of 0 to 8 and the other is the wavelength of 0 to 12 - so that to create ZERO the meaning of 1 had to be phase shifted based on the noncommutative phase truth of reality. Infinity was 12 to 0 for the 12/8 wavelength as geometric magnitude and Infinity was 0 to 12 for the 8/12 wavelength as 3/2 frequency but infinity was 0 to 8 for the 3/4 wavelength as 4/3 geometric magnitude. Or G=3=F at the same time due to noncommutative phase as the 5th dimension.

What Philolaus called the Subcontrary Mean was 6/8 wavelength as 4/3 geometric magnitude as frequency of 0 to 8 root tonic and then Archytas covered up the wavelength part by changing the name of Subcontrary Mean to Harmonic Mean so that it was just frequency as geometric magnitude from 12 to 0, the opposite direction and different root tonic.

And so to bring this a step further - the Ditonic Comma is then linked to the Ditone which is linked to another "comma" -  as Wiki puts in their footnote:

diatonic comma, better known as syntonic comma, equal to the frequency ratio 81:80

But what Wiki doesn't tell you is that Diatonic Comma was created by Archytas by first assuming that the Perfect Fifth is squared or 3/2 is inherently a squared number.

However, he [Archytas] noted that the product of the arithmetic mean and the harmonic mean is equal to the square of the geometric mean, so this gave a way of dividing the fifth of 3:2 into the product of 5:4 and 6:5.

A Truman State University review on Scriba, Christoph J. “Mathematics and music.” (Danish)
Normat 38 (1990), no. 1, 3–17, 52.

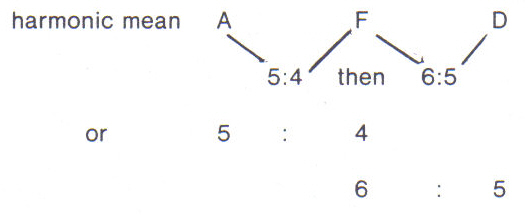6/5 (harmonic mean) x 5/4 (arithmetic mean) = Perfect Fifth as Geometric Mean Squared

Another definition of 3/2 as the Perfect Fifth developed in the birth of modern science - the 16th Century - as the "mean fifth" or the fourth root of 5 which equals 1.495 to create the Diatonic Comma of 81/80.  Since 81/80 is the amount by which Didymus corrected the Pythagorean major third 81:64, to a just major third 5:4. But this made the two fifths dissonant between the major third and root tonic so C to E as 5/4. So 81/64 is actually from Philolaus using 9/8 squared, not the 81:64 ditone is 3^4/2^6 (or 3/1 * 3/1 * 3/1 * 3/1 * 1/2 * 1/2 * 1/2 * 1/2 * 1/2 * 1/2).

The Monochord in Ancient Greek Harmonic Science

https://books.google.com/books?isbn=0521843243

David Creese - 2010 - ‎History

This new paran ̄et ̄e, standing for the moment two whole tones below n ̄et ̄e, must then be sharpened slightly to produce a 'sweetened' major third; Archytas will have assigned this interval the ratio 5:4 (the nearest epimoric smaller than the ditone: (9:8)squared = 81:64 and 5:4 = 80:64).

 a product of Archytas equation – with 9/8 cubed approximating the square root of two!

“The sound of square roots

Take two strings, one sounding an octave higher than the other, so that their lengths are in the ratio 2:1. Then find the geometric ratio (also called the mean proportional) between these strings, the length x at which 2:x is the same proportion as x:1. This means that 2:x = x:1; cross-multiplying this gives x squared =2. Thus, the “ratio” needed is √2:1 ≈ 1.414, in modern decimals. This is close to the dissonant interval called the tritone, which later was called the “devil in music,” namely the interval composed of three equal whole steps each of ratio 9:8. The tritone is thus 9:8 × 9:8 × 9:8 = 729:512 ≈ 1.424.” from “Scandal of the Irrational” M.I.T. Press. pdf link here

"... the tyrant in the Republic as the tyrant's suffering is exactly 729 times that of a philosopher, using the metaphor of ... The ratio 729/512, three whole tones (8:9) above 512....“Since 9 actually reduces to a wholetone of 9/8, its cube will reduce to (9/8)³ = 729/512, a [FAKE] Pythagorean approximation to the square root. of two, a problem which fascinated Socrates in the marriage allegory.” Ernest McClain, The Pythagorean Plato: Prelude to the Song Itself (Nicholas-Hays, 1978), p. 36

 So you have 8 to the 6th power and 9 to the 6th power (531441) as the secret of the Ditonic Comma as the fake Pythagorean Comma due to geometric mean. From Euclid and earlier from Philolaus and Archytas as 8 to the 6th compared to 9 to the 6th which assumes that the starting root tonic "frequency" as the 1 is 8 to the 6th which is already from assuming the Perfect Fifth is squared!

 

Lore and Science in Ancient Pythagoreanism

https://books.google.com/books?isbn=0674539184

Walter Burkert - 1972 - ‎Literary Criticism

to this, the apotome would be 2187: 2048, and the komma 531441 : 524288 — pure frivolity.41 Philolaus' treatment is different:42 He establishes as the basis of tone the number which first makes the cube of the first odd number and was highly honored among the Pythagoreans [i.e., 27] ... a number which is separated by a ...

The Science of Harmonics in Classical Greece

https://books.google.com/books?isbn=1139468626

Andrew Barker - 2007 - ‎Philosophy

It is again obvious that Philolaus is not thinking in terms of ratios alone. The ratio of the komma can be computed;it is 531441:524288, but this–in Burkert's phrase– is 'pure frivolity'.21 Boethius has already told us, in fact (Inst. mus. 3.5), that Philolaus identified the komma [531441 : 524288 aka the Ditonic Comma] with the unit, 1, as being the difference between a diesis ...

From the Beginning to Plato - Page 269 - Google Books Result

https://books.google.com/books?isbn=0415062721

Christopher Charles Whiston Taylor - 1997 - ‎Reference

The 'diesis' should be 256:243 and the 'comma' 531441:524288. Neither of these intervals can be divided in half in the sense of the Sectio Canonis. Since Philolaus seems clearly to recognize that the tone cannot be divided in half, it is rather surprising that he apparently takes for granted—what is false in terms of the ..

In Egypt, problem 50 of Ahmes is that a square field of side 8 units is equal to a circle of diameter 9 units with 4 x (8/9) squared closely approximating the transcedental (pi). (Source: Makers of Mathematics). So PI only assumes a logarithmic definition of 9/8 from music theory!

By relying on reversing the order of the natural number ratios, so that the minor sixth was 8:5 and the major third was 5:4 – not the major third as 4:5, the natural extension of the Tetrad there was a crucial switch from Pythagorean shamanism to the Freemasonic Golden Ratio behind science. This amazing secret of the Greek Miracle is detailed in “The Minor Sixth (8:5) in Early Greek Harmonic Science,” by Alan C. Bowen, The American Journal of Philology, 1978:

Any who doubt that the musical ratios are all of greater inequality, i.e., that the antecedent or first term in each is greater than the consequent or second term, should consult Archytas DK 47 B 2. This Fragment…requires that the ratios be of this form if the assertions about the three means [arithmetic, harmonic and geometric] are to be true. Accordingly, the ratios assigned to the octave, fifth, fourth and minor sixth, must be 2:1, 3:2, 4:3 and 8:5, and not 1:2, 2:3, 3:4 and 5:8, respectively, as Mosshammer and others would have them….Indeed, there is early proof deriving from the Pythagorean school that intervals, such as the fifths, which are represented by superparticular ratios cannot be partitioned into any number of equal subintervals because the terms of these ratios admit no number of geometric means….Consider now the question of the status of the ratio (8:5) in the Pythagorean harmonic science that dates from the late fifth century B.C. to the time of Apollodorus. One should not expect that this ratio was recognized as melodic by every school of Pythagorean musical theory. For example those who sought to derive all the musical ratios from the Tetrad of the decad by compounding and dividing the ratios of the primary and most familiar intervals, the concords of the octave, fifth and fourth, would find the minor sixth unascertainable….There is reason to believe that these were supplied by Archytas in the early fourth century B.C.

Professor Micahel J. B. Allen (UCLA) in his “Ficino, Daemon Mathematics and the Spirit” in the book Natural Particulars (M.I.T. Press, 1999) documents that the founder of humanism, Marsilio Ficino discovered in Plato a secret demonstration of the 5/4 as cube root of two transformation.

At first the 12 × 30 = 360 system proved extremely useful in ancient Sumeria and even way back in the beginning of monoculture, rectilinear plow agriculture in 9,000 B.C.E. Armenia (which had a 36 letter gematria alphabet) because the second way of construction was used — simply an average of the two natural numbers 4:5. As music professor Ernest McClain writes in his book The Myth of Invariance and his online essays on the ratio 4:5 and the Lunar calendar — the Gods of the ancient world WERE ratios and the 60 number system enabled a means to standardize the 1:2:3:4:5 ratios since all are factors of 60. The God of the ratio 30:60 was the Lunar God — Sin — in ancient Sumeria, just as for Chinese harmonics, the Moon is 1/2 as the first octave with the Sun as 3/2 and 2/3.

And so it either takes a mystic musician really thinking about the mystery of the Pythagorean Tetraktys and thereby studying and training with a REAL CHINESE spiritual master alchemist or it takes a real deep math professor (Fields Medal) to reveal the solution to this fundamental error of the Music-Math-Physics Trifecta in the West. I'm talking about Alain Connes of course.

a “universal scaling system”, ... this discrete scaling manifests itself in acoustic systems, as is well known in western classical music, where the two scalings correspond, respectively, to passing to the octave (frequency ratio of 2) and transposition (the perfect fifth is the frequency ratio 3/2), with the approximate value log(3)/ log(2) ∼ 19/12 responsible for the difference between the “circulating temperament” of the Well Tempered
Clavier and the “equal temperament” of XIX century music. It is precisely the irrationality of log(3)/ log(2) which is responsible for the noncommutative [complementary opposites as yin/yang] nature of the quotient corresponding to the three places {2, 3,∞}. - Alain Connes

So what is he talking about? We just got Wikipedia and some fancy integer continued fraction sequence encyclopedia explaining that the Pythagorean Comma IS the Ditonic Comma - but they both ASSUME a commutative logarithmic foundation of reality. Connes DOES NOT because he has really thought deeply about the math AND the physics.

"There is a fine structure in spacetime, exactly as there is a fine structure in spectrals [frequencies].... The idea is to replace a geometric space with an algebra, as an inverse of the Dirac operator, by sending a wave with a constraint on the vibration of the wave, can not vibrate faster than 1, the commutator of the Dirac Operator is less than 1....The spectrum of the Dirac Operator...space is not simply a manifold but multiplied by a noncommutative finite space. There is behind the scene, there is a square root and when you take a square root there is an ambiguity and the ambiguity that is there is from the spin structure....Finite space which is there is essentially the simplest finite space which has dimension zero, as far as the [frequency] spectrum is concerned...."

 Alain Connes on Music youtube lecture

 So what Connes is stating is that for every "zero" point in space there is actually a noncommutative phase that is the 5th dimension of reality - and this is also what the Pythagoreans and Chinese and Indian alchemists were referring to and developed a whole body-mind training science based on this ancient truth.

 Nick and Greg - Lee Fang just got the IF Stone award for his excellent reporting and he exposed how the "X-box generation" is buying guns along with Vampire and Zombie practice targets - at shooting ranges. And so the gun industry is marketing towards this Slenderman insanity instead of "hunters." But I exposed recently how this goes back to Philolaus and Plato and Archytas. What Philolaus did was flip his Lyre around and so lied about the Lyre - thereby turning infinite time-frequency energy as noncommutative phase (the secret truth of reality as Alain Connes, Fields Medal math professor points out) into irrational magnitude symmetric math. The trick works like this. We are taught Octave = Perfect Fifth plus Perfect Fourth but that assumes that 9/4 is not 3/2 doubled or multiplied by 2 but rather 3/2 squared. So that the Perfect Fifth - the Perfect Fourth = 9/8 as the major 2nd music tone. You Punk Rock musicians (like I was) of course know the 1-4-5 music chords that defines PUNK. But we all got PUNKED by Plato promoting the lies of ARchytas and Philolaus. So what Philolaus had to do was flip his Lyre around - I go into the details on my blog - but that is how "zero" was created, it assumes geometric magnitude or defining infinity as a negative materialistic idealism. It literally creates hell on Earth - if you understand alchemy like I do and math professor Abraham Seidenberg promoted this as the Separation of Heaven and Earth as mass ritual sacrifice geometry.

Managing the Math Deluge: A Conversation with Edward Dunne

www.ams.org/notices/201505/rnoti-p522.pdf

In August 2014, Edward. G. Dunne became execu- tive editor of Mathemat- ical Reviews (MR). He succeeded Graeme Fair- weather, who had been in the post since 2008 and has now retired. Dunne is well known in the mathematical com- munity for his work on the AMS book pro- gram: He was an AMS acquisitions editor .

 Dear Dr. Dunne: Below is what I posted on my blog today http://ecoechoinvasives.blogspot.com - Thanks for your nice research that I disagree with. Please let me know any comments, criticisms or questions - I have more details on my blog, drew hempel, MA

Forwarded to Mark McConnell and Dave Rusin - all math professors focused on music tuning.

Dear folks in NYC on LaMonte Young natural harmonics. I did my master's thesis on this topic in 2000 and then I did intensive Daoist alchemy meditation based on music theory from Chunyi Lin spiritual healer who trained at Shaolin and did 40 day nonstop full lotus meditation, no sleep, in a cave at Mt. Qingcheng. So then I kept studying in full lotus, reading 1 scholarly book a day for 10 years. I have a blog that has all my research details http://ecoechoinvasives.blogspot.com So Alain Danielou made a big mistake about his Pythagorean Comma since he assumes that the Ditonic Comma is the same as the Pythagorean Comma and so he assumes a logarithmic definition of 9/8 as 3/2 squared but the Orthodox Pythagorean philosophy and Daoist alchemy harmonics did not do this.

The trick is also for the Daoists, the 1 root tonic is also the Moon energy and this has to do then - with the actual Pythagorean comma being the difference between the Moon and Sun calendar. And so there is an alchemy meditation of 12 notes along the body-mind - and this is the real Pythagorean harmonics since each note gets its Perfect Fifth as the inversion from the opposite direction of infinite. NOT the squaring and dividing by 2 averaging of Philolaus and Archytas and Plato - the fake Pythagoreans promoted by the West by Ernest McClain, Joscelyn Godwin, etc. So Alain Danileou was very close to the truth but still relying on this problematic math. But Alain Connes did figure out the truth as noncommutative phase! So did Eddie Oshins, as quantum physicist at Stanford Linear Accelerator Center who also taught Wing Chun. He realized the secret of Daoist Neigong alchemy is from noncommutative phase. He did not realize that the spin 1/2 resonance harmonics are also from Pythagorean music theory - but Alain Connes has made this connection.

Anyway I have more details - much more - on my blog - it's all free research.

thanks,

drew hempel, MA