Hypatia Reincarnated? Finally a good calculus teacher but is there a FIXED POINT IN TIME? No.

So everyone enjoys a young pretty calculus female teacher who gives coy, caddy comments like "just humor me" as she explains the secret trick of the derivative.

And so then 90% of the comments are about how pretty the teacher is, but someone gets honest:

Shouldn't the second Y coordinate equal the first Y coordinate + the distance between the first and second y coordinate? Not the distance between X and (h+x)?

And he does not get a good response at all! This is the great "bait and switch" of math. So what is the real answer to this innocent question?

 Good question. I think the trick is explained here:

"Then A has coordinates (1, b+m)."

 http://www2.clarku.edu/~djoyce/trig/tangents.html

So secant is the ratio of hypotenuse (x + h) over adjacent - that goes to the limit of x as zero as the tangent point.

You can see that the point 1 unit to the right of the origin is labeled 1, and its coordinates, of course, are (1,0). Let C be the point where that vertical line cuts the horizontal line through B. Then C has coordinates (1,b).

The point A is where the vertical line above 1 cuts the original line. Let m denote the distance that A is above C. Then A has coordinates (1,b+m). This value m is called the slope of the line. If you move right one unit anywhere along the line, then you’ll move up m units.
Now consider the angle CBA. Let’s call it the angle of slope. It’s tangent is CA/BC = m/1 = m. Therefore, the slope is the tangent of the angle of slope.

 And so we can see what just happened - the Y value got reduced, as a function of time, to a limit of zero as a pure geometric magnitude "point" of no dimension! Aka "m."

Now that's just Trig and so it's not fancy enough for the real "bait and switch" needed for calculus. So we need the real answer right?

I mean obviously I must be missing something? No not really - this is the secret trick of calculus and our lovely Hypatia just revealed it for all.

Secant Lines, Tangent Lines, and Limit Definition of a Derivative 

So in the vid above she says the secant becomes the tangent - as the limit of the secant slope. She moves her hand as a magic trick! She was really trying to do the above gif.


But that really doesn't capture the bait and switch as I just showed from Trig - no it does exactly what she did - a fancy moving motion that covers up the conversion of time into a geometric zero point.

So now we have to go into the mathematical logic of how this is derived!

Let's throw up another gif.

 

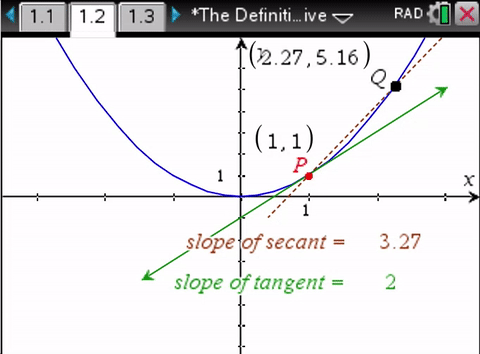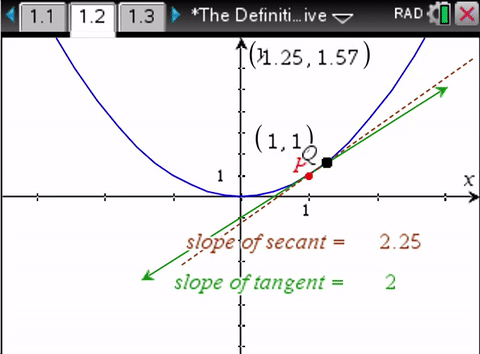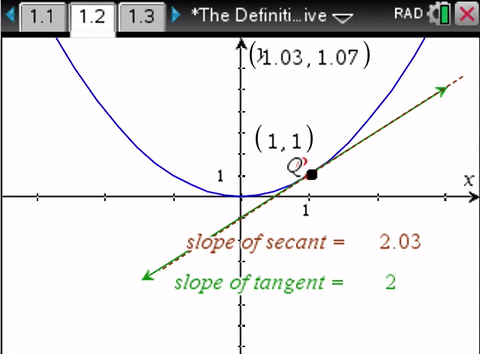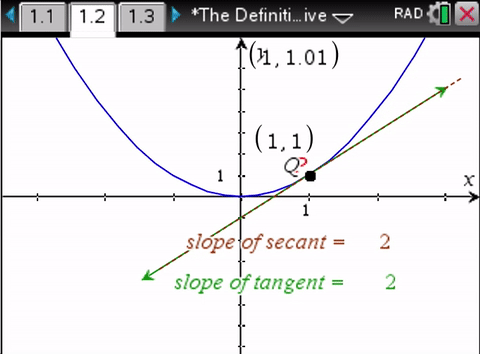
This seems a little better since there are numbers added to the geometry but essentially it's a divide and average bait and switch, with change of X reducing to a function of Y as zero time.

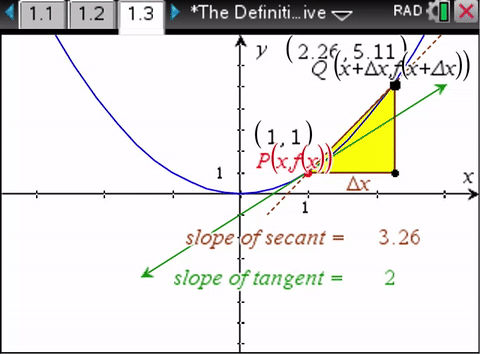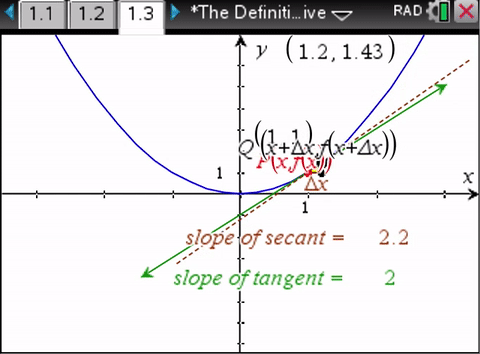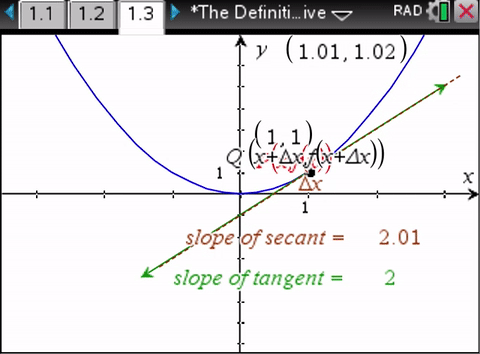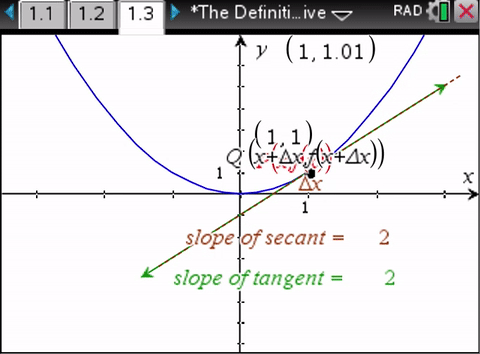
We don’t need calculus to determine the slope of the secant line. We do need calculus to determine the slope of the tangent line.

So the bait and switch.

Now let's look at the actual math derivation - the logic involved behind the bait and switch. I just showed it from Trig - there the bait and switch is out in the open. I challenged the Kaplans about the very same problem of assuming a commutative value of a geometric point with a one to one conversion to number. In other words is infinity a symmetric inversion to zero? No.

So now we get another young female pretty voice - but just the voice with a video.

And so she explains we can find the slope of the tangent using the limiting process - as long as it is a "fixed point" (in time).

 And that my friends is the bait and switch. There is no "fixed point in time." There is eternal motion. The only way we can experience a true "fixed point" is if there is no space at all - when light is turned around back on to itself - but this creates reverse time energy as noncommutative phase - the superluminal pilot wave from the future!

Next we will look at noncommutative calculus.